ノーベル賞を取った投資理論
現代のファイナンス理論
1952年、シカゴ大学の大学生ハリー・マーコウィッツは、博士論文のテーマに株式を選びました。彼は株価というのはルーレットやサイコロのように、上がったり下がったりランダムに決まるもので、全ては確率で決定されるのではないかと考えた、これを「効率的市場仮説」と言う。そこで確率計算や統計学を使う事を思い付く。
1827年、ロバート・ブラウンは水に浮かんだ花粉が奇妙な動きをしているのに気付いた。この動きの謎は1905年にアインシュタインによって、熱運動する媒質の分子の不規則な衝突によって引き起こされる現象である事が確認されました。このでたらめな動きをブラウン運動と呼び、マーコウィッツは株価の動きもこのブラウン運動と似たようなものではないかと考えたのです。
リスクというのは損する可能性を表す言葉ではなく、予測可能性を表す言葉です。リスクが低いというのは予測可能性が高く、リスクが高いというのは予測可能性が低い事を表します。つまり、リスクと期待リターンは1対1で対応しており、リスクが低いというのは儲かる可能性も低く、リスクが高ければ儲かる可能性も高い。リスクは儲かったり損したりする可能性を言うのですから。
マーコウィッツは個々の株にはそれぞれリスクが存在しており、正反対のリスク特性を持つ銘柄同士を保有すれば、打ち消し合う波のようにリスクを軽減させながら、期待リターンは高く維持出来るのではないかと考えました。そして彼は株式投資の世界で昔から有効とされてきた「分散投資」の効用を数学的に証明したのです。これがモダンポートフォリオ理論です。
マーコウィッツの発見は、リスクが低い銘柄(電力株など)とリスクが高い銘柄(IT銘柄など)を組み合わせる事で、たった一つの銘柄に全額投資するよりも低いリスクで高いリターンを得られる、というものでした。とはいえ、組み合わせのパターンは沢山あるし、その人の経済状況によっても取れるリスクには違いがあります。
プロの証券マンはそういった点を挙げ、だから自分達にお金を払って、自分にピッタリのポートフォリオを作りませんかと言ってきます。確かに素人の自分が考えるよりも、経済状況からプロにオーダーメイドのポートフォリオを作ってもらう方が無難でしょう。それが伝統的な証券マンの仕事内容だったのです。
しかし、イェール大学で教鞭を執っていたジェームズ・トービンは、どんな人だろうと株式銘柄の保有比率は同じでよいと言い出しました。トービンは大事なのは銘柄ではなく、各々のリスク許容度に合わせて株式と国債(無リスク資産)の割合を決める事だと主張したのです。これを効率的ポートフォリオと呼びます。
そしてウィリアム・F・シャープが「資本資産価格モデル:CAPM(キャップエム)」という理論を提唱します。シャープは値動きの要素は
- 銘柄固有の動きα
- 株式市場の銘柄が感応する動きβ
- 予測不可能な出来事
の3つであり、分散投資は3を消し去る効果がある。ならば値動きは1と2で決まるが1のαは一定であり、リターンは最終的にβで決定されると主張したのです。さらにここから効率的ポートフォリオは世界に一つしかなく、それは世界の株式市場の縮小コピーであると結論付けたのです。
上記の3人は、それぞれノーベル経済学賞を受賞しました。
効率的市場仮説は正しいのか
多くの学者達によって最終的に導き出された最も正しい投資方法は、
インデックスファンドを買えばいいだけ
というものだったのです。しかし、これはプロの証券マンからしたら一大事です。彼らの仕事は顧客に合わせてオーダーメイドのポートフォリオを作りお金を貰う事ですから、効率的市場仮説が正しいとすれば、株のプロなど不要になるからです。そこで株のプロ達は、理論の前提となる効率的市場仮説を集中砲火するようになりました。
効率的市場仮説とは、市場は効率的であり、株価は将来に対する情報を既に織り込んだ状態になっているという仮説です。つまり、割安株があったとしてもめざとい投資家達がすぐに見つけ出し食い潰してしまうため、株価に影響を与える情報は瞬時に株価に取り込まれ、どんなテクニックを用いても恒常的に利益を上げ続ける事は不可能というわけです。
インデックス投資家のバイブルとも言うべき「ウォール街のランダム・ウォーカー」の中で、著者バートン・マルキールはこれを端的に表すジョークを紹介しています。
効率的市場理論を信奉するファイナンスの教授と学生が交わす有名なジョークから始めよう。お札を見つけた学生が立ち止まって拾おうとすると、教授はそれをたしなめて、「よしたまえ。もしそれが本物のお札なら、今まで放置されているはずがないだろう」と言った。(第10版p334)
ウォーレン・バフェット、ピーター・リンチのように大儲けした投資家もいるじゃないか、投機家として勝ち続けたラリー・ウィリアムズはどう説明するんだ等、色々な反論がありますが、結局のところ株をやる人は儲けようと思って買うわけですから、最終的なパフォーマンスを比較すればどちらの陣営が正しいかはすぐに分かります。
市場そのものに投資しているインデックスファンドと、ファンドマネージャーが分析、調査をして売買銘柄を決定し運用しているアクティブファンド、どちらが儲かっているのでしょうか。投資の本場アメリカでは、何度となく金融のプロ達が運用するアクティブファンドと市場平均(インデックスファンド)のパフォーマンスが比較されてきましたが、一貫してアクティブファンドはインデックスファンドに勝てないという結果が出ています。
中には市場平均を超えるパフォーマンスを出すファンドも現れますがそれは少数であり、しかもそういったファンドも毎年恒常的に市場平均を上回る事は出来ないのです。インデックスファンドと比べてアクティブファンドは手数料などのコストが高くつきます。市場が効率的であれば誰も未来を予測出来ませんから、高コストの分だけどうしても不利になるのです。
中には毎年市場平均を超えるアクティブファンドは無いかも知れないが、超えるファンドが存在する事は確かである。そういったファンドを選べば市場平均よりも儲ける事は可能だ、と主張しますが、どのファンドが儲かるかなど事前にどうやって知るのでしょうか。そんな未来予測が出来る人間なら値上がりする株も分かるでしょうし、わざわざ高い手数料を払ってファンドを買わずに直接株式を購入するでしょう。
世界株ポートフォリオとは
世界経済は拡大し続けている
旧時代は社会主義と資本主義がぶつかり、どちらが正しいのか争っていました。代表的なのはソ連とアメリカでしょう。しかし、社会主義は失敗しソ連は解体されロシアとなり、アメリカは今でも超大国として君臨しています。かつては社会主義を採用していた国々の多くが資本主義へと舵を切り、発展途上国の多くが経済発展してきています。
資本主義は自己増殖するシステムですから、世界が資本主義を採用する限り、世界経済は拡大し続ける事になります。しかし、気を付けなければいけないのは、全ての株が上がったりはしないという事です。個々の株が上がったり下がったり株価はランダムウォークするが、全体としてみれば市場は拡大を続けるという意味であり、そしてそれは株だけではなく国も同じであり、ファイナンス理論で言う市場とは世界全体を指しているのです。
世界を丸ごと買ってしまおう
日本の株価指数で代表的なのは日経平均とTOPIXですが、当然世界中の市場にも株価指数は存在します。NYダウ平均、S&P500、ナスダック総合指数などです。他にも発展著しい新興国向けの株価指数もあります。しかし、一国丸ごと購入するのは一銘柄購入するよりは安全かもしれませんが、その国自体の経済が悪化すればマイナスになりますし、新興国の場合は上げ下げが激しくバブルが置きやすいという懸念もあります。
モダンポートフォリオ理論では可能な限りの分散投資が有効であると証明し、CAPM理論は株式市場の縮小コピーこそ最高のポートフォリオであると結論づけました。ならば一国の株式市場を買うのではなく、世界の株式市場を時価総額の割合で購入する事が最適だという結論になります。これが世界株ポートフォリオです。
リーマンショックのように世界経済自体が大打撃を受けたらどうするのかと言う人もいるでしょうが、その時はどんな投資をしていても損しているでしょうから気にしてもしょうがありません。例え一時停滞したとしても持ち直す可能性は高い、人類の経済規模は拡大し続けてきたからです。リーマンショックでさえ一年後には世界経済は元のレベルに戻りました。もし世界経済がまだ成長し続けるはずだと考えるのなら、世界市場を丸ごと購入する投資方法が最も経済合理的ではないでしょうか。
世界株ポートフォリオを説明した書籍では、「臆病者のための株入門 (文春新書) 」が最も平易な一冊。
他にはベストセラーとなった「ほったらかし投資術」があります。
簡単にできる世界株投資
かつて日本では個々の国を対象としたインデックスファンドしかなかく、先進国インデックスファンド(日本を除く)、日本国インデックスファンド、新興国インデックスファンドを個別に、その時の時価総額に合わせた割合を購入し、1年に1回程度リバランス(割合の調整のための買い直し)をしていました。
嬉しいことに現在では、買えば世界株ポートフォリオが実現するインデックスファンド(またはETF)が販売されています。最も代表的なのはアメリカバンガード社のバンガード・トータル・ワールド・ストックETF(通称VT)です。これ1本で世界の株式市場を丸ごと購入できます。
日本ではeMAXIS Slim全世界株式(オール・カントリー)(通称オルカン)が最も有名。この2本はやっている事は同じですがカバー率に違いがあります。VTは全世界の時価総額98%以上をカバーしているのに対し、オルカンは約85%。しかし、おおよそ同じ値動きですから、そこまで気にする事はないでしょう。また、信託報酬はVTが0.07%、オルカンは0.05775%と安い。購入の敷居の低さから今から世界株投資をするのなら、日本人にとってオルカンが第一候補となるでしょう。
ドル・コスト平均法
機関投資家やミリオネアでもない一般的な人々は、日々の生活があるため一度に大金を投資する事は出来ません。投資はあくまで余剰資金で行うものであり、生活を圧迫するような無謀な投資は誰も行わないでしょう。そういった一般人が投資を行うとしたら必然的に「積立投資」になります。
積立投資でよく出てくるのが「ドル・コスト平均法」です。これは定期的に一定の金額を投資し続ける投資法で、ファンドは値動きしますから結果的に高い時は少し買い、安い時には多く買うという事になり、平均購入単価を低く抑える効果があると言われています。
しかし、こんなものは株のナンピン買いと同じじゃないかと批判する人もいます。確かにいくらリスクを分散するといっても、買っているファンドが値下がりしかしなければリスクを分散させようが損するだけです。ドル・コスト平均法はあくまで長期的に値上がりしていかない限り儲からないという事です。
それでも長期的な積立投資をするのならドル・コスト平均法は有用なツールになるでしょう、なぜなら何も考えなくていいからです。人間考えすぎると悪い手を打ってしまいがちです。ファンドの値動きに一喜一憂しておかしな売買を繰り返してしまったり、仕事や趣味の時間を食い潰して投資戦略を考え過ぎたり。ドル・コスト平均法は単に平均購入単価を抑えるという以外にも、精神安定と貴重な時間の浪費を防ぐ効果があるのです。
さらに証券会社によっては、設定をする事で毎月銀行口座から決まった金額を自動積立してくれるサービスを実施しているところもあります。これなら最初に投資プランを決めて設定すれば、後は何もする事はありません。毎日仕事をし趣味を楽しんでいればいつの間にか投資は完了しているのです。
これ以外にもドル・コスト平均法に工夫を加えた「バリュー・アベレージング法」というのもあります。
理想のアセットアロケーションは?
株式は世界株ポートフォリオで持つとして、全体の資産はどのように保有するかという問題があります。絶対的な正解はありませんが、よく言われるのが「財産三分法」です。これはユダヤの聖典タルムードに書かれている事で、財産は土地に1/3、商品(株式)に1/3、現金に1/3にすべしという教えです。
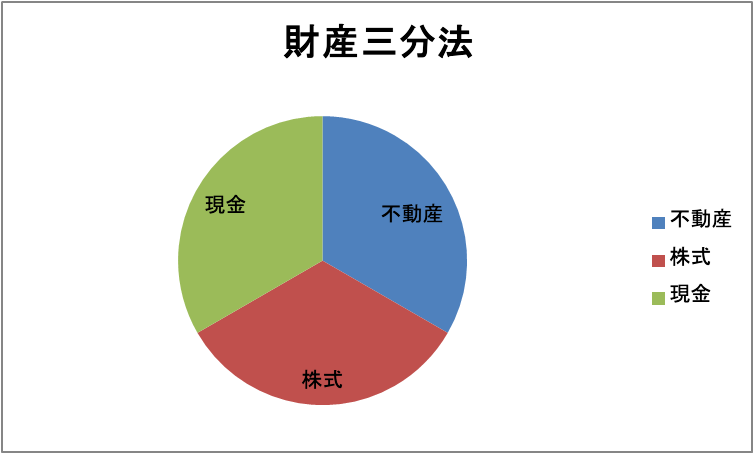
1000万円の資産があれば、土地(REIT)に約333万円、株式に約333万円、現金で333万円保有する事になります。他にもバートン・マルキール氏の「財産4分法」というのもあります。これは年齢により不動産等、ポートフォリオの比率を変化させる投資法です。詳しくは「ウォール街のランダム・ウォーカー 」をお読み下さい。
自分のリスク許容度を測る
標準偏差とは
標準偏差(S.D.)は統計からどれ位データがばらけているかを数値で表した指標です。およそ標準偏差1つ分の中に68%のデータが、標準偏差2個分の中に95%のデータが入るそうです。2個分を超えるほど多かったり少なかったりするデータは残りの5%”特殊なデータ”と見なされます。平均値と標準偏差が分かればデータのばらつきをある程度把握する事が可能になります。
期待リターンとリスクから耐えられるか調べる
投資信託にはよくこう書いてあります。
- 期待リターン年○%
- リスク(標準偏差)年○%
例えば期待リターン5%、リスク15%だとして、期待リターンを中心に据え、そこからリスク(標準偏差)1個分(ー10%~20%)に収まる可能性が68%、リスク(標準偏差)2個分(ー25%~35%)に収まる可能性が95%、それに収まらない確率が5%という事になります。そしてそれを図で表したものを正規分布(ベルカーブ)と言います。
自分が耐えられる値下がり幅を設定し、期待リターンと標準偏差を元に投資信託が一年でどれだけ、何%の確率で下がるのか計算した上で購入を検討するとよいでしょう。
コア・サテライト戦略とは
コア・サテライト戦略は、ポートフォリオを攻めと守りの二つに分けて運用するやり方です。コア(核)部分はインデックス投資や債券などの安定した投資を行い、サテライト(衛星)部分は新興国株や商品先物などリスクを取って高パフォーマンスを狙います。
難しい表現になっていますが、要は安定的な投資を基本として、少しハイリスクな投資で冒険もしてみましょうという投資法です。コア80%、サテライト20%という比率が最も多いようです。
インデックス投資は何も考えないのでつまらないと思う人は、コア・サテライト戦略を使いインデックス投資を全体の80%行い、残りの20%でテクニカル分析やファンダメンタルズ分析を駆使して、自ら銘柄の売買を行うのもいいでしょう。失敗しても致命的な損失にはならないでしょうし、無理だと思えば100%インデックス投資に切り替えればいいだけです。
6つの係数を使おう
終価係数表
終価係数表は現在保有する金融資産を○%で複利運用した場合、何年後にいくらになるか調べるための早見表です。
終価係数 = (1 + 年利率)^年数
例えば100万円を年利5%で10年複利運用するなら、5%と10年が交差した1.629を100万円に掛けると計算出来ます。この場合は
1,000,000 × 1.629 = 1,629,000円
になります。
| 1% | 2% | 3% | 4% | 5% | 6% | 7% | 8% | 9% | 10% | |
| 1年 | 1.01 | 1.02 | 1.03 | 1.04 | 1.05 | 1.06 | 1.07 | 1.08 | 1.09 | 1.1 |
| 2年 | 1.02 | 1.04 | 1.061 | 1.082 | 1.103 | 1.124 | 1.145 | 1.166 | 1.188 | 1.21 |
| 3年 | 1.03 | 1.061 | 1.093 | 1.125 | 1.158 | 1.191 | 1.225 | 1.26 | 1.295 | 1.331 |
| 4年 | 1.041 | 1.082 | 1.126 | 1.17 | 1.216 | 1.262 | 1.311 | 1.36 | 1.412 | 1.464 |
| 5年 | 1.051 | 1.104 | 1.159 | 1.217 | 1.276 | 1.338 | 1.403 | 1.469 | 1.539 | 1.611 |
| 6年 | 1.062 | 1.126 | 1.194 | 1.265 | 1.34 | 1.419 | 1.501 | 1.587 | 1.677 | 1.772 |
| 7年 | 1.072 | 1.149 | 1.23 | 1.316 | 1.407 | 1.504 | 1.606 | 1.714 | 1.828 | 1.949 |
| 8年 | 1.083 | 1.172 | 1.267 | 1.369 | 1.477 | 1.594 | 1.718 | 1.851 | 1.993 | 2.144 |
| 9年 | 1.094 | 1.195 | 1.305 | 1.423 | 1.551 | 1.689 | 1.838 | 1.999 | 2.172 | 2.358 |
| 10年 | 1.105 | 1.219 | 1.344 | 1.48 | 1.629 | 1.791 | 1.967 | 2.159 | 2.367 | 2.594 |
| 11年 | 1.116 | 1.243 | 1.384 | 1.539 | 1.71 | 1.898 | 2.105 | 2.332 | 2.58 | 2.853 |
| 12年 | 1.127 | 1.268 | 1.426 | 1.601 | 1.796 | 2.012 | 2.252 | 2.518 | 2.813 | 3.138 |
| 13年 | 1.138 | 1.294 | 1.469 | 1.665 | 1.886 | 2.133 | 2.41 | 2.72 | 3.066 | 3.452 |
| 14年 | 1.149 | 1.319 | 1.513 | 1.732 | 1.98 | 2.261 | 2.579 | 2.937 | 3.342 | 3.797 |
| 15年 | 1.161 | 1.346 | 1.558 | 1.801 | 2.079 | 2.397 | 2.759 | 3.172 | 3.642 | 4.177 |
| 16年 | 1.173 | 1.373 | 1.605 | 1.873 | 2.183 | 2.54 | 2.952 | 3.426 | 3.97 | 4.595 |
| 17年 | 1.184 | 1.4 | 1.653 | 1.948 | 2.292 | 2.693 | 3.159 | 3.7 | 4.328 | 5.054 |
| 18年 | 1.196 | 1.428 | 1.702 | 2.026 | 2.407 | 2.854 | 3.38 | 3.996 | 4.717 | 5.56 |
| 19年 | 1.208 | 1.457 | 1.754 | 2.107 | 2.527 | 3.026 | 3.617 | 4.316 | 5.142 | 6.116 |
| 20年 | 1.22 | 1.486 | 1.806 | 2.191 | 2.653 | 3.207 | 3.87 | 4.661 | 5.604 | 6.727 |
現価係数表
現価係数は将来の額から現在必要になる額を求める時に使用する係数です。
現価係数 = (1 + 年利率)^(年数 × -1)
例えば20年後に1000万円作るとして、年利5%で複利運用する場合
10,000,000 × 0.3769 = 3,769,000円
必要になるという事です。
| 1% | 2% | 3% | 4% | 5% | 6% | 7% | 8% | 9% | 10% | |
| 1年 | 0.9901 | 0.9804 | 0.9709 | 0.9615 | 0.9524 | 0.9434 | 0.9346 | 0.9259 | 0.9174 | 0.9091 |
| 2年 | 0.9803 | 0.9612 | 0.9426 | 0.9246 | 0.9070 | 0.8900 | 0.8734 | 0.8573 | 0.8417 | 0.8264 |
| 3年 | 0.9706 | 0.9423 | 0.9151 | 0.8890 | 0.8638 | 0.8396 | 0.8163 | 0.7938 | 0.7722 | 0.7513 |
| 4年 | 0.9610 | 0.9238 | 0.8885 | 0.8548 | 0.8227 | 0.7921 | 0.7629 | 0.7350 | 0.7084 | 0.6830 |
| 5年 | 0.9515 | 0.9057 | 0.8626 | 0.8219 | 0.7835 | 0.7473 | 0.713 | 0.6806 | 0.6499 | 0.6209 |
| 6年 | 0.9420 | 0.8880 | 0.8375 | 0.7903 | 0.7462 | 0.7050 | 0.6663 | 0.6302 | 0.5963 | 0.5645 |
| 7年 | 0.9327 | 0.8706 | 0.8131 | 0.7599 | 0.7107 | 0.6651 | 0.6227 | 0.5835 | 0.547 | 0.5132 |
| 8年 | 0.9235 | 0.8535 | 0.7894 | 0.7307 | 0.6768 | 0.6274 | 0.5820 | 0.5403 | 0.5019 | 0.4665 |
| 9年 | 0.9143 | 0.8368 | 0.7664 | 0.7026 | 0.6446 | 0.5919 | 0.5439 | 0.5002 | 0.4604 | 0.4241 |
| 10年 | 0.9053 | 0.8203 | 0.7441 | 0.6756 | 0.6139 | 0.5584 | 0.5083 | 0.4632 | 0.4224 | 0.3855 |
| 11年 | 0.8963 | 0.8043 | 0.7224 | 0.6496 | 0.5847 | 0.5268 | 0.4751 | 0.4289 | 0.3875 | 0.3505 |
| 12年 | 0.8874 | 0.7885 | 0.7014 | 0.6246 | 0.5568 | 0.497 | 0.444 | 0.3971 | 0.3555 | 0.3186 |
| 13年 | 0.8787 | 0.773 | 0.681 | 0.6006 | 0.5303 | 0.4688 | 0.415 | 0.3677 | 0.3262 | 0.2897 |
| 14年 | 0.87 | 0.7579 | 0.6611 | 0.5775 | 0.5051 | 0.4423 | 0.3878 | 0.3405 | 0.2992 | 0.2633 |
| 15年 | 0.8613 | 0.743 | 0.6419 | 0.5553 | 0.481 | 0.4173 | 0.3624 | 0.3152 | 0.2745 | 0.2394 |
| 16年 | 0.8528 | 0.7284 | 0.6232 | 0.5339 | 0.4581 | 0.3936 | 0.3387 | 0.2919 | 0.2519 | 0.2176 |
| 17年 | 0.8444 | 0.7142 | 0.605 | 0.5134 | 0.4363 | 0.3714 | 0.3166 | 0.2703 | 0.2311 | 0.1978 |
| 18年 | 0.836 | 0.7002 | 0.5874 | 0.4936 | 0.4155 | 0.3503 | 0.2959 | 0.2502 | 0.212 | 0.1799 |
| 19年 | 0.8277 | 0.6864 | 0.5703 | 0.4746 | 0.3957 | 0.3305 | 0.2765 | 0.2317 | 0.1945 | 0.1635 |
| 20年 | 0.8195 | 0.673 | 0.5537 | 0.4564 | 0.3769 | 0.3118 | 0.2584 | 0.2145 | 0.1784 | 0.1486 |
減債基金係数表
減債基金係数表は目標額に対し、毎月いくら積み立てればいいか分かる早見表です。
減債基金係数 = 年利率 ÷ (((1 + 年利率)^年数) – 1)
例えば3000万円の資産を利回り5%、20年掛けて作りたいとするなら、5%と30年が交差する0.03024を3000万円に掛ければいいだけです。
30,000,000 × 0.03024 = 907,200円
毎年907,200円、毎月75,600円積み立てればいい事が分かります。
| 1% | 2% | 3% | 4% | 5% | 6% | 7% | 8% | 9% | 10% | |
| 1年 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2年 | 0.49751 | 0.49505 | 0.49261 | 0.4902 | 0.4878 | 0.48544 | 0.48309 | 0.48077 | 0.47847 | 0.47619 |
| 3年 | 0.33002 | 0.32675 | 0.32353 | 0.32035 | 0.31721 | 0.31411 | 0.31105 | 0.30803 | 0.30505 | 0.30211 |
| 4年 | 0.24628 | 0.24262 | 0.23903 | 0.23549 | 0.23201 | 0.22859 | 0.22523 | 0.22192 | 0.21867 | 0.21547 |
| 5年 | 0.19604 | 0.19216 | 0.18835 | 0.18463 | 0.18097 | 0.1774 | 0.17389 | 0.17046 | 0.16709 | 0.1638 |
| 6年 | 0.16255 | 0.15853 | 0.1546 | 0.15076 | 0.14702 | 0.14336 | 0.1398 | 0.13632 | 0.13292 | 0.12961 |
| 7年 | 0.13863 | 0.13451 | 0.13051 | 0.12661 | 0.12282 | 0.11914 | 0.11555 | 0.11207 | 0.10869 | 0.10541 |
| 8年 | 0.12069 | 0.11651 | 0.11246 | 0.10853 | 0.10472 | 0.10104 | 0.09747 | 0.09401 | 0.09067 | 0.08744 |
| 9年 | 0.10674 | 0.10252 | 0.09843 | 0.09449 | 0.09069 | 0.08702 | 0.08349 | 0.08008 | 0.0768 | 0.07364 |
| 10年 | 0.09558 | 0.09133 | 0.08723 | 0.08329 | 0.0795 | 0.07587 | 0.07238 | 0.06903 | 0.06582 | 0.06275 |
| 11年 | 0.08645 | 0.08218 | 0.07808 | 0.07415 | 0.07039 | 0.06679 | 0.06336 | 0.06008 | 0.05695 | 0.05396 |
| 12年 | 0.07885 | 0.07456 | 0.07046 | 0.06655 | 0.06283 | 0.05928 | 0.05590 | 0.0527 | 0.04965 | 0.04676 |
| 13年 | 0.07241 | 0.06812 | 0.06403 | 0.06014 | 0.05646 | 0.05296 | 0.04965 | 0.04652 | 0.04357 | 0.04078 |
| 14年 | 0.0669 | 0.06260 | 0.05853 | 0.05467 | 0.05102 | 0.04758 | 0.04434 | 0.0413 | 0.03843 | 0.03575 |
| 15年 | 0.06212 | 0.05783 | 0.05377 | 0.04994 | 0.04634 | 0.04296 | 0.03979 | 0.03683 | 0.03406 | 0.03147 |
| 16年 | 0.05794 | 0.05365 | 0.04961 | 0.04582 | 0.04227 | 0.03895 | 0.03586 | 0.03298 | 0.0303 | 0.02782 |
| 17年 | 0.05426 | 0.04997 | 0.04595 | 0.04220 | 0.0387 | 0.03544 | 0.03243 | 0.02963 | 0.02705 | 0.02466 |
| 18年 | 0.05098 | 0.04670 | 0.04271 | 0.03899 | 0.03555 | 0.03236 | 0.02941 | 0.0267 | 0.02421 | 0.02193 |
| 19年 | 0.04805 | 0.04378 | 0.03981 | 0.03614 | 0.03275 | 0.02962 | 0.02675 | 0.02413 | 0.02173 | 0.01955 |
| 20年 | 0.04542 | 0.04116 | 0.03722 | 0.03358 | 0.03024 | 0.02718 | 0.02439 | 0.02185 | 0.01955 | 0.01746 |
資本回収係数
ローンの年間返済額を求めたり、元本を一定利率で複利運用しながら、毎年一定額を一定期間取り崩して毎年いくら受け取れるか、つまり現在の資金額から受取年金額を求めるのに使います。
資本回収係数 = 年利率 ÷ (1 – ((1 + 年利率)^(年数 × -1)))
例えば現在の1500万円を年利5%で20年間複利運用しながら取り崩す場合、5%と20年の交差する0.08024を掛けます。
15,000,000 × 0.08024 = 1,203,600円
年間1,203,600円、毎月100,300円取り崩せるという事になります。
| 1% | 2% | 3% | 4% | 5% | 6% | 7% | 8% | 9% | 10% | |
| 1年 | 1.01 | 1.02 | 1.03 | 1.04 | 1.05 | 1.06 | 1.07 | 1.08 | 1.09 | 1.1 |
| 2年 | 0.50751 | 0.51505 | 0.52261 | 0.5302 | 0.5378 | 0.54544 | 0.55309 | 0.56077 | 0.56847 | 0.57619 |
| 3年 | 0.34002 | 0.34675 | 0.35353 | 0.36035 | 0.36721 | 0.37411 | 0.38105 | 0.38803 | 0.39505 | 0.40211 |
| 4年 | 0.25628 | 0.26262 | 0.26903 | 0.27549 | 0.28201 | 0.28859 | 0.29523 | 0.30192 | 0.30867 | 0.31547 |
| 5年 | 0.20604 | 0.21216 | 0.21835 | 0.22463 | 0.23097 | 0.2374 | 0.24389 | 0.25046 | 0.25709 | 0.2638 |
| 6年 | 0.17255 | 0.17853 | 0.1846 | 0.19076 | 0.19702 | 0.20336 | 0.2098 | 0.21632 | 0.22292 | 0.22961 |
| 7年 | 0.14863 | 0.15451 | 0.16051 | 0.16661 | 0.17282 | 0.17914 | 0.18555 | 0.19207 | 0.19869 | 0.20541 |
| 8年 | 0.13069 | 0.13651 | 0.14246 | 0.14853 | 0.15472 | 0.16104 | 0.16747 | 0.17401 | 0.18067 | 0.18744 |
| 9年 | 0.11674 | 0.12252 | 0.12843 | 0.13449 | 0.14069 | 0.14702 | 0.15349 | 0.16008 | 0.1668 | 0.17364 |
| 10年 | 0.10558 | 0.11133 | 0.11723 | 0.12329 | 0.12950 | 0.13587 | 0.14238 | 0.14903 | 0.15582 | 0.16275 |
| 11年 | 0.09645 | 0.10218 | 0.10808 | 0.11415 | 0.12039 | 0.12679 | 0.13336 | 0.14008 | 0.14695 | 0.15396 |
| 12年 | 0.08885 | 0.09456 | 0.10046 | 0.10655 | 0.11283 | 0.11928 | 0.12590 | 0.13270 | 0.13965 | 0.14676 |
| 13年 | 0.08241 | 0.08812 | 0.09403 | 0.10014 | 0.10646 | 0.11296 | 0.11965 | 0.12652 | 0.13357 | 0.14078 |
| 14年 | 0.0769 | 0.0826 | 0.08853 | 0.09467 | 0.10102 | 0.10758 | 0.11434 | 0.1213 | 0.12843 | 0.13575 |
| 15年 | 0.07212 | 0.07783 | 0.08377 | 0.08994 | 0.09634 | 0.10296 | 0.10979 | 0.11683 | 0.12406 | 0.13147 |
| 16年 | 0.06794 | 0.07365 | 0.07961 | 0.08582 | 0.09227 | 0.09895 | 0.10586 | 0.11298 | 0.12030 | 0.12782 |
| 17年 | 0.06426 | 0.06997 | 0.07595 | 0.08220 | 0.08870 | 0.09544 | 0.10243 | 0.10963 | 0.11705 | 0.12466 |
| 18年 | 0.06098 | 0.06670 | 0.07271 | 0.07899 | 0.08555 | 0.09236 | 0.09941 | 0.1067 | 0.11421 | 0.12193 |
| 19年 | 0.05805 | 0.06378 | 0.06981 | 0.07614 | 0.08275 | 0.08962 | 0.09675 | 0.10413 | 0.11173 | 0.11955 |
| 20年 | 0.05542 | 0.06116 | 0.06722 | 0.07358 | 0.08024 | 0.08718 | 0.09439 | 0.10185 | 0.10955 | 0.11746 |
年金現価係数
将来、希望する年金額を受け取るための必要原資を求める時に使用する係数です。
年金現価係数 = (1 – ((1 + 年利率)^(年数 × -1))) ÷ 年利率
例えば年利5%で複利運用しながら、毎年120万円ずつ20年間年金を受け取りたい場合
1,200,000 × 12.462 = 14,954,400円
となります。つまり、14,954,400円を5%で運用しながら、毎月10万円ずつ取り崩していくと、丁度20年で無くなるという事です。
| 1% | 2% | 3% | 4% | 5% | 6% | 7% | 8% | 9% | 10% | |
| 1年 | 0.99 | 0.98 | 0.971 | 0.962 | 0.952 | 0.943 | 0.935 | 0.926 | 0.917 | 0.909 |
| 2年 | 1.97 | 1.942 | 1.913 | 1.886 | 1.859 | 1.833 | 1.808 | 1.783 | 1.759 | 1.736 |
| 3年 | 2.941 | 2.884 | 2.829 | 2.775 | 2.723 | 2.673 | 2.624 | 2.577 | 2.531 | 2.487 |
| 4年 | 3.902 | 3.808 | 3.717 | 3.63 | 3.546 | 3.465 | 3.387 | 3.312 | 3.24 | 3.17 |
| 5年 | 4.853 | 4.713 | 4.58 | 4.452 | 4.329 | 4.212 | 4.1 | 3.993 | 3.89 | 3.791 |
| 6年 | 5.795 | 5.601 | 5.417 | 5.242 | 5.076 | 4.917 | 4.767 | 4.623 | 4.486 | 4.355 |
| 7年 | 6.728 | 6.472 | 6.23 | 6.002 | 5.786 | 5.582 | 5.389 | 5.206 | 5.033 | 4.868 |
| 8年 | 7.652 | 7.325 | 7.02 | 6.733 | 6.463 | 6.21 | 5.971 | 5.747 | 5.535 | 5.335 |
| 9年 | 8.566 | 8.162 | 7.786 | 7.435 | 7.108 | 6.802 | 6.515 | 6.247 | 5.995 | 5.759 |
| 10年 | 9.471 | 8.983 | 8.53 | 8.111 | 7.722 | 7.36 | 7.024 | 6.71 | 6.418 | 6.145 |
| 11年 | 10.368 | 9.787 | 9.253 | 8.76 | 8.306 | 7.887 | 7.499 | 7.139 | 6.805 | 6.495 |
| 12年 | 11.255 | 10.575 | 9.954 | 9.385 | 8.863 | 8.384 | 7.943 | 7.536 | 7.161 | 6.814 |
| 13年 | 12.134 | 11.348 | 10.635 | 9.986 | 9.394 | 8.853 | 8.358 | 7.904 | 7.487 | 7.103 |
| 14年 | 13.004 | 12.106 | 11.296 | 10.563 | 9.899 | 9.295 | 8.745 | 8.244 | 7.786 | 7.367 |
| 15年 | 13.865 | 12.849 | 11.938 | 11.118 | 10.38 | 9.712 | 9.108 | 8.559 | 8.061 | 7.606 |
| 16年 | 14.718 | 13.578 | 12.561 | 11.652 | 10.838 | 10.106 | 9.447 | 8.851 | 8.313 | 7.824 |
| 17年 | 15.562 | 14.292 | 13.166 | 12.166 | 11.274 | 10.477 | 9.763 | 9.122 | 8.544 | 8.022 |
| 18年 | 16.398 | 14.992 | 13.754 | 12.659 | 11.69 | 10.828 | 10.059 | 9.372 | 8.756 | 8.201 |
| 19年 | 17.226 | 15.678 | 14.324 | 13.134 | 12.085 | 11.158 | 10.336 | 9.604 | 8.95 | 8.365 |
| 20年 | 18.046 | 16.351 | 14.877 | 13.59 | 12.462 | 11.47 | 10.594 | 9.818 | 9.129 | 8.514 |
年金終価係数
年金終価係数は定期的に定額複利運用で積み立てた時、将来いくらになるか表す係数です。
年金終価係数 = (((1 + 年利率)^年数) – 1) ÷ 年利率
年利回り5%の複利運用で、毎年36万円を積み立てた場合、20年後には
360,000 × 33.066 = 11,903,760円
となります。
| 1% | 2% | 3% | 4% | 5% | 6% | 7% | 8% | 9% | 10% | |
| 1年 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2年 | 2.01 | 2.02 | 2.03 | 2.04 | 2.05 | 2.06 | 2.07 | 2.08 | 2.09 | 2.1 |
| 3年 | 3.03 | 3.06 | 3.091 | 3.122 | 3.153 | 3.184 | 3.215 | 3.246 | 3.278 | 3.31 |
| 4年 | 4.06 | 4.122 | 4.184 | 4.246 | 4.31 | 4.375 | 4.44 | 4.506 | 4.573 | 4.641 |
| 5年 | 5.101 | 5.204 | 5.309 | 5.416 | 5.526 | 5.637 | 5.751 | 5.867 | 5.985 | 6.105 |
| 6年 | 6.152 | 6.308 | 6.468 | 6.633 | 6.802 | 6.975 | 7.153 | 7.336 | 7.523 | 7.716 |
| 7年 | 7.214 | 7.434 | 7.662 | 7.898 | 8.142 | 8.394 | 8.654 | 8.923 | 9.2 | 9.487 |
| 8年 | 8.286 | 8.583 | 8.892 | 9.214 | 9.549 | 9.897 | 10.26 | 10.637 | 11.028 | 11.436 |
| 9年 | 9.369 | 9.755 | 10.159 | 10.583 | 11.027 | 11.491 | 11.978 | 12.488 | 13.021 | 13.579 |
| 10年 | 10.462 | 10.950 | 11.464 | 12.006 | 12.578 | 13.181 | 13.816 | 14.487 | 15.193 | 15.937 |
| 11年 | 11.567 | 12.169 | 12.808 | 13.486 | 14.207 | 14.972 | 15.784 | 16.645 | 17.56 | 18.531 |
| 12年 | 12.683 | 13.412 | 14.192 | 15.026 | 15.917 | 16.87 | 17.888 | 18.977 | 20.141 | 21.384 |
| 13年 | 13.809 | 14.68 | 15.618 | 16.627 | 17.713 | 18.882 | 20.141 | 21.495 | 22.953 | 24.523 |
| 14年 | 14.947 | 15.974 | 17.086 | 18.292 | 19.599 | 21.015 | 22.55 | 24.215 | 26.019 | 27.975 |
| 15年 | 16.097 | 17.293 | 18.599 | 20.024 | 21.579 | 23.276 | 25.129 | 27.152 | 29.361 | 31.772 |
| 16年 | 17.258 | 18.639 | 20.157 | 21.825 | 23.657 | 25.673 | 27.888 | 30.324 | 33.003 | 35.95 |
| 17年 | 18.43 | 20.012 | 21.762 | 23.698 | 25.84 | 28.213 | 30.84 | 33.75 | 36.974 | 40.545 |
| 18年 | 19.615 | 21.412 | 23.414 | 25.645 | 28.132 | 30.906 | 33.999 | 37.45 | 41.301 | 45.599 |
| 19年 | 20.811 | 22.841 | 25.117 | 27.671 | 30.539 | 33.76 | 37.379 | 41.446 | 46.018 | 51.159 |
| 20年 | 22.019 | 24.297 | 26.87 | 29.778 | 33.066 | 36.786 | 40.995 | 45.762 | 51.16 | 57.275 |
GPIFの憂鬱
本当は利益を上げているGPIF
GPIF(Government Pension Investment Fund)は年金積立金管理運用独立行政法人を指します。GPIFは国民年金と厚生年金の積立金を運用する日本の年金基金です。最近このGPIFに対する風当たりが強いようです。理由は単純で国民が積み立てた年金を無能な運用で損失を発生させているというものです。
GPIFは2007年度と2008年度で約15兆円の損失を出しました。この頃のマスコミは「素人の官僚が運用するな」「国民の金でギャンブルをやっている」などサディスティックな批判を加えていました。では今までの通算運用成績は大きく元本を減らしたのかというと、自主運用を開始した2001年から累積収益額で132兆4,113億円の黒字を計上しているのです(2023年度第3四半期)。
GPIFは市場平均に勝つ事は極めて難しいと発言している通り、基本はインデックス投資を行っています。2007年といえばリーマンショックにより世界経済そのものが大打撃を受けた時期であり、どんな投資を行っていても大概は大きな損失を出していたのです。
マスコミは損失が出た時は大きく報道しますが、利益が出た時は報道しない、したとしてもとても小さな記事で報道します。損失が出た時に国民の不安を増大させる報道をしたマスコミは、その後の運用成績に関してもしっかり報道する責任があるのではないでしょうか。
GPIFのポートフォリオは?
アセットアロケーションとは資産配分を表す用語です。GPIFは2020年4月1日からの5カ年の基本ポートフォリオとして以下の組成を採用しています。
国内株式 25%
国内債券 25%
外国株式 25%
外国債券 25%
GPIFの期待リターンとリスク
自らのリスク許容度に合わせてポートフォリオを組もうとした時に、先進国株式や新興国株式の期待リターンとリスクを知りたいと思うでしょう。しかし絶対の基準は無いというのが答えになりますが、いくつか有名なデータは存在します。その中に日本では最も有名なのがGPIFのデータでしょう。
GPIF(2020年度からの第4期中期計画(5ヵ年計画))
| 期待リターン | リスク(標準偏差) | |
|---|---|---|
| 国内債券 | 0.7% | 2.56% |
| 国内株式 | 5.6% | 23.14% |
| 外国債券 | 2.6% | 11.87% |
| 外国株式 | 7.2% | 24.85% |
| 短期金利 | 0.6% | – |
これが必ず正しいという保証はありませんが、個人投資家などは一番参考にしているようです。こういったデータは他にも「KKR(国家公務員共済組合連合会)」「ニッセイ基礎研究所」「みずほ信託銀行」などがデータを公開しています。
アナリストは当てにならない?
株はプロのいない世界
プロというとどんな人物を思い描くでしょうか。アマと比べて強い人、それで賞金などを稼ぎ生計を立てている人、人により様々でしょうが、共通するのはその分野で非常に優秀な人物という点でしょう。
株の世界にもアナリストやファンドマネージャーと呼ばれるプロが存在しています。多くの人が彼らを信じ、新聞や雑誌の有名アナリストの株価予測を読み、実際の売買の参考にします。彼らは難しい数式や投資理論を駆使して株価予想を行い、私達の資産運用の手助けをしてくれます。しかし、ここで一つの疑問が浮かびます。
「なぜ彼らは親切にも儲かる情報を他人に教えてくれるんだろう?」
理由は単純明快で彼らの言う事を聞いても儲からないからです。本当に儲かる情報をなぜ他人に教える必要があるでしょうか? 他人に教えるくらいなら自分で儲けてしまうはずです。
株はゼロサムゲームであり誰かが得すれば誰かが損する世界なのです。原理的に参加者全てが儲ける事は出来ません。わざわざ教えてくれるという事は、すなわち彼らが自分達には未来の株価なんて分からないという告白なのです。
プロのいる世界とは逆でプロのいない世界も存在します。例えばコイン投げやサイコロ振りなどです。こういったものは何が出るかは偶然で決まるため、事前に予測出来る人などいません(イカサマが無い限り)。
効率的市場仮説が正しいとすれば、株の世界もコイン投げやサイコロ振りと同じであり、全ては偶然により決まるのだからプロなどいるはずがない。だからこそただの主婦とかニートが何億円と儲けたり出来るのです。偶然性が弱いプロが存在する世界ではこんな事はあり得ない。算数の成績1の人物が、大学の数学教授に偶然勝つなどあり得ないでしょう。
これを裏付けるデータもあります。アメリカでは何度となく市場平均とプロのファンドマネージャーが運用するファンドのパフォーマンスが比較されてきました。その結果は長期的に見るとアクティブファンドの6~7割は市場平均に負けているというものでした。アクティブファンドは人件費などにより割高な手数料の分だけどうしても不利になるのです。これはアメリカだけに限った事ではなく日本でも同じです。1996年~2005年で市場平均をアクティブファンドの半数が超えられたのは4回だけだったという結果が出ています。
カリスマトレーダーの正体
彼らが実際は株価がどうなるか分からず、適当な事を専門用語でそれっぽく言っているだけなら、なぜ彼らは失業しないのでしょうか? ファンドマネージャーといった金融のプロは明らかにホワイトカラーであり、優秀な人物なら年収何千万という世界です。嘘しか言わない役立たずならすぐお払い箱になるはずです。
これは株の世界に限った話ではなく、他の多くの世界で見掛ける評論家と呼ばれる人種に共通して見られる事ですが、彼らは自分達を優秀に見せるいくつかの手口を使い、その地位を安定させているのです。
まず適当な予想をします。人は平和な話より恐怖を煽る話に食いつくため、そういう予想にします。例えば「3年後、日本のGDPは10%低下している」と言ったとしましょう。そして3年後、本当にその通りになったら自分は3年前に予測していたと騒ぎます。誰も予想出来なかった日本経済の未来をズバリ当てた人間として話題になるでしょう。
外した場合は黙っておきます。正解が出るのは3年後なんですから誰も覚えていません。つまり皆当たった事した覚えていない。こういった詐欺みたいな予想を専門用語を散りばめてそれっぽく主張すればいいだけです。何度もやればカリスマ評論家になれるでしょう。
しかし、あまりにも外れが続けば流石に信用を失います。そこで全て二元論で予想するのが賢明です。○○は成功するか失敗するか、結果は2通りしかないのでコイン投げと全く同じ。適当に言っても半分は当たるわけです。
それでもアクティブファンドが儲かりそうな気がする
証券会社の広告などを見ていると、やっぱりプロの運用するファンドは儲かっているという印象を受けるかも知れません。証券会社は年に何本も新たな投信を発売し、その中の好成績を残した投信だけを宣伝するため、プロはやっぱり凄いという印象を受けるだけです。
成績が悪ければ宣伝しませんし、最悪償還してしまいます。償還とは売れない、解約が相次いだなどの理由で純資産総額が少なくなって、投信自体が消滅してしまうという事です。なぜ売れなかったり解約が相次ぐのかは言わずもがなです。
参考図書



コメント