A*アリゴリズムとは
A*アルゴリズムは経路探索アルゴリズムの一種。ゲームでは敵に自機を追いかけさせたり、プレイヤーのクリック地点にキャラクターを移動させたりなどの実装に使われる。A*アルゴリズムの内容を備忘録として記録。
ノード
格子状に作られた1つ1つのマス目のこと。A*アルゴリズムではマス目、タイルなどではなくノードと呼ぶ。
スタートノードとゴールノード
処理を始める最初がスタートノード、目的地のノードがゴールノード。
現在ノード
今、選択中の隣接ノードを調べるノード。親ノードの次のノードであり、現在ノードの前が親ノード。
特定ノード
現在ノードの隣接ノードの中の、今コストを計算しようとしている特定のノード。
親ノード
ある特定ノードで隣接ノードを調べていくとき、その元(手前)のノードを親とする(例えば、あるノードAからノードBに移動した場合、ノードAがノードBの親ノードとなる)。そのためゴールノードに到着したとき、ゴールノードの親からノードを辿って行けばゴールノードからスタートノードまでの経路が分かる。親ノードはオープンした各ノードにそれぞれ設定される。
親ノードを記録するタイミングは、
- 初めてノードをオープンリストに追加する時
- 既にオープンリストにあるノードのコストが更新された時
コスト
各ノードが経路(ゴールに向かう道筋)にどれだけ近いか表す数値。コストが大きいノードより、小さいノードが好ましい(近い)。
g
スタートノードからある特定のノードまでのコスト。スタートノードから特定のノードまでは正確な経路を知っているため、このコストは正確に計算できる。
h
特定のノードからゴールノードまでにかかるだろう推定コスト(ヒューリスティック)。先の正確な経路はまだ分からないため、推定にすぎない。
f
特定のノードの総コストで、f = g + hで計算する。
オープンリスト
オープンリストには既に開かれた(コスト計算済み)のノードが登録される。オープンリストは次に探索するノードを選択するための候補を提供する。
オープンリスト内のノードは、fに基づいて優先順位が付けられる。最小コストのノードが優先的に選ばれる。
計算済みノードのgと比べて、現在ノードから見て再計算されたgがより小さい値になった場合、ノードのgが更新され、親ノードも現在ノードに再設定される。
クローズドリスト
クローズドリストには、一度現在ノードとなり評価されたノードが追加される。クローズドリストは再度同じノードを評価することを防ぎ、無駄な計算を避ける。
クローズドリストに追加されたノードは、今後の探索から除外されるため、アルゴリズムの効率が向上。これにより探索空間が縮小し、計算時間が短縮される。
A*アルゴリズムの手順
- 初期化スタートノードをオープンリストに追加し、gを0、h、fを計算。
- ノードの選択オープンリストからfが最小のノードを選択。このノードを現在ノードとする。
- 終了条件の確認現在ノードがゴールノードであれば、経路を再構築し探索を終了。オープンリストにノードが見付からない(空)場合、探索を終了。
- 特定ノードの評価現在ノードに隣接する特定ノード全てをコスト計算する。各特定ノードに対し以下を行う。
- 通行禁止区域またはクローズドリスト追加済みノードの場合
- この特定ノードは無視し、別のノードに移る。
- オープンリストに無いの場合
- この特定ノードをオープンリストに追加。
- 現在ノードをこの特定ノードの親にする。
- この特定ノードのg、h、fを計算する。
- オープンリストに有るの場合
- 現在ノードから見て再計算されたgが、計算済みのgよりも小さい場合、gを更新し、親ノードを現在ノードに変更。
- 通行禁止区域またはクローズドリスト追加済みノードの場合
- 現在ノードの移動現在ノードをオープンリストから削除し、クローズドリストに追加。これにより既に評価したノードを再評価しないようにする。
- 繰り返し手順2から手順5を、ゴールノードが見付かるまで繰り返す。
- 結果の再構築ゴールノードに到達したら、ゴールノードにとっての親ノードを辿り、そのまた親ノードを辿ることでスタートノードまで遡る。この経路がスタートノードからゴールノードまでの最短経路になる。
コスト計算の方法
或る特定のノードのコストは「f = g + h」で計算する。gはそのノードまでのコスト、hはそのノードからゴールまでの推定コスト。
gの求め方は、スタートノードからそのノードまでに辿ったノード数を用いる。或るノードから周辺ノードまでは1の移動コストがかかることにする。つまりスタートノードの周辺ノードにはコスト1が割り振られる。

周辺ノードのさらに周辺ノードのコストは2となる。

但し、上下と斜めでは斜めの方が距離が離れている。斜めは1.414(2の平方根)のため、正確には直進の移動コストは1、斜め移動のコストは1.4で計算。
ユークリッド法
hの求め方は今回はユークリッド法を使用。ピタゴラスの定理を用い2点間の行と列の数を数え、2乗し、足し、平方根を求める(正確な距離が知りたいわけではないため、平方根を求めずそのままの数値でも利用できる)。
dx = 列の距離
dy = 行の距離
h = Math.sqrt(dx * dx + dy * dy)ノードのコストfをg + hで求める。
他にもマンハッタン法(市街地距離法)、対角線法などがある。
マンハッタン法
ユークリッド法と違い斜め移動のない経路探索。2つのノードの列の差、行の差を足すだけでいい。ノードの計算量が多くなる。
マンハッタン法は他の発見的手法と違い、縦横の移動だけで斜め移動しない。碁盤の目状の市街地(マンハッタンの様な)を移動する動きで経路探索することからこの名称となっている。
h = Math.abs(列の距離) * 直進の移動コスト + Math.abs(行の距離) * 直進の移動コスト対角線法
3つの中で最もノードの計算量が少ない。
dx = Math.abs(列の距離)
dy = Math.abs(行の距離)
diag = Math.min(dx, dy)
straight = dx + dy
h = 斜め移動のコスト * diag + 直進の移動コスト * (straight - 2 * diag)処理の流れを図解
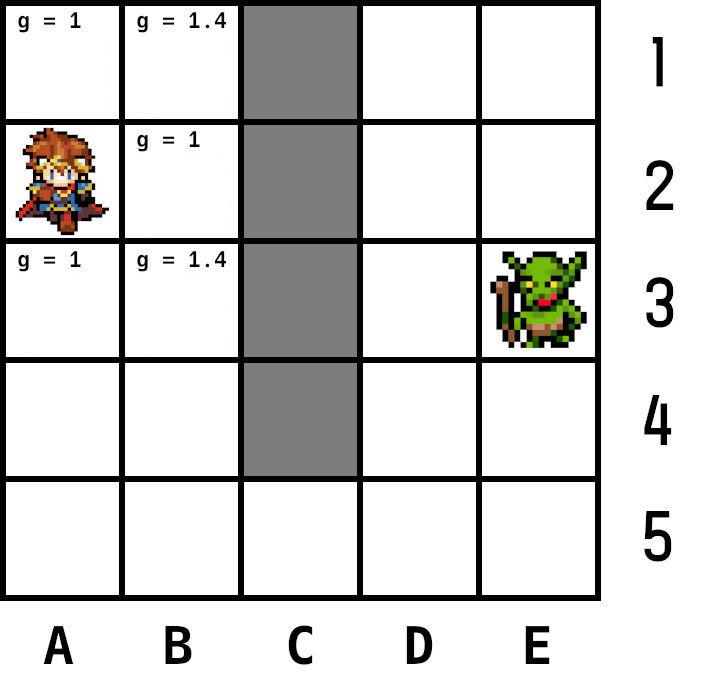
下の画像は5×5マスの領域。勇者のいるノード(A2)がスタートノード、ゴブリンのいるノード(E3)がゴールノード。塗り潰されたノードは壁(進入禁止区域)。

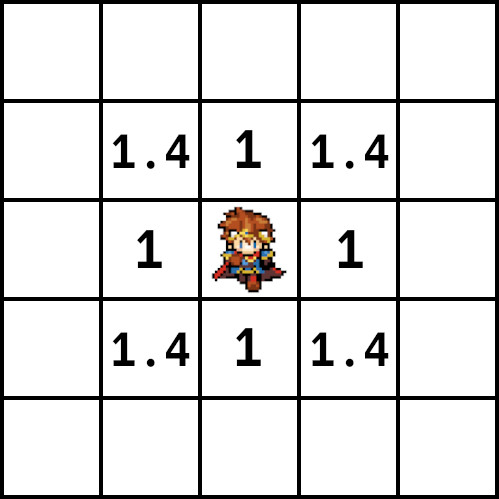
まずgから計算する。上下のノードはコスト1、斜めのノードは1.4とする。
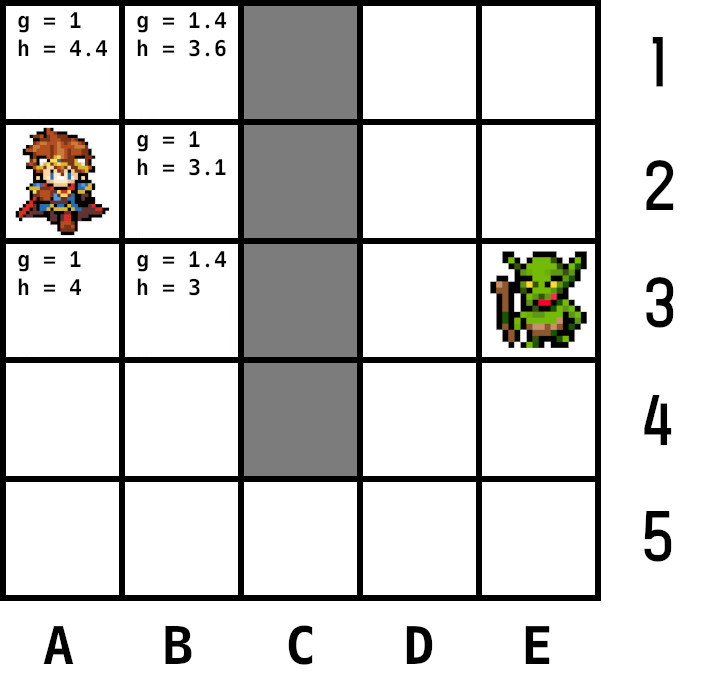
次にhを計算する。2点間のノードの数を単位として(ピクセルではない)行と列でピタゴラスの定理を使い計算。例えば、勇者の1つ上のノード(A4)からゴールであるゴブリンのノード(E3)へは、行(横)で4ノード、列で2ノード。4 × 4 ⁺ 2 × 2 = 20で平方根は4.4、これがhの値となる。
全ての周辺ノードを計算したら、最後にgとhを足しfを求める。
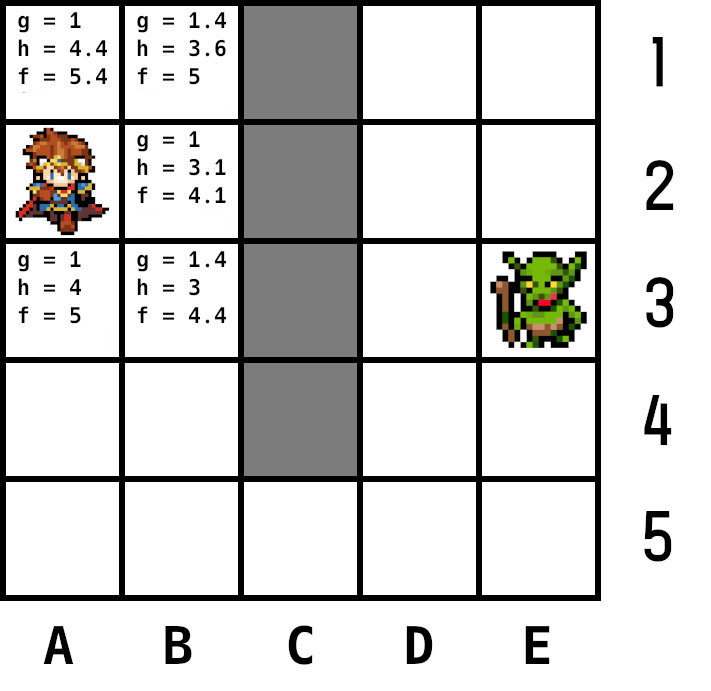
計算した各隣接ノードをオープンリストに追加し、それぞれに現在ノード(A2)を親ノードに登録。
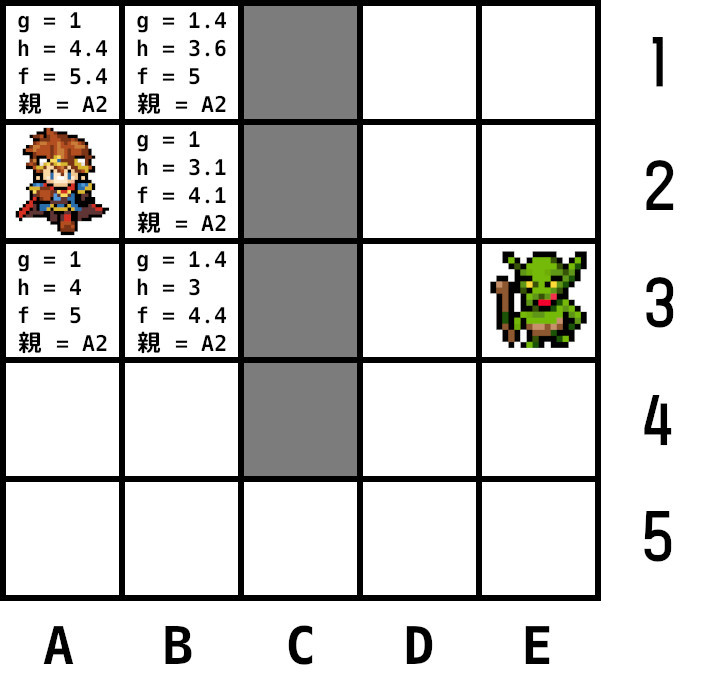
現在ノードをオープンリストから削除し、クローズドリストに追加。クローズドリストに追加されたノードは2度と評価されない。
手順2に戻る。オープンリストから最小コストのノードを探す。ここではB2のノードとなる。これを現在ノードに変更。
赤はクローズドリスト入り、青はオープンリスト入り、緑は現在ノード。
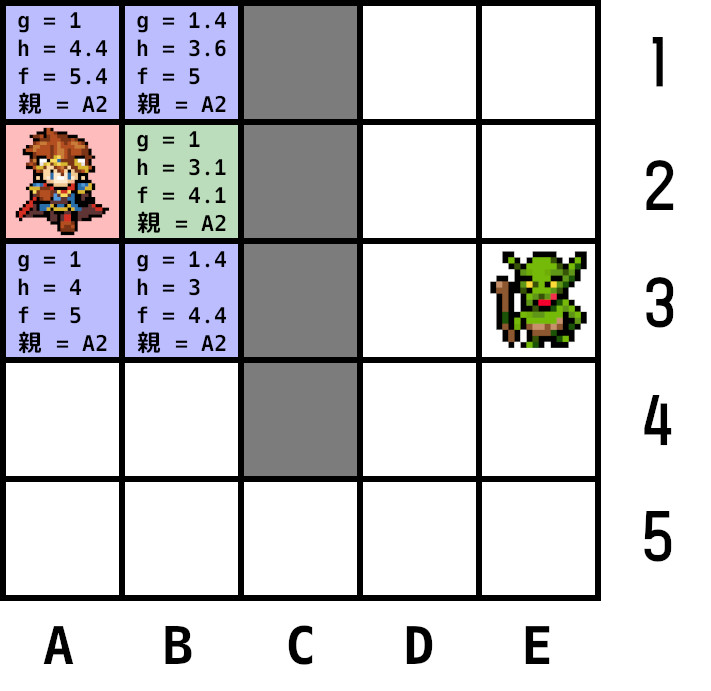
B2の隣接ノードはスタートノードを除いて、全てオープンリスト追加済みのため、現在ノードから見てgを再計算し、その結果、元のgよりも値が小さければ入れ替えfを再計算する。
上の例ではB2から見て、A1、B1、A3、B3全て元のgより値が大きくなるため更新しない。
オープンリスト内のノードで最小コストはB3。B3を現在ノードとし隣接ノードを計算する。
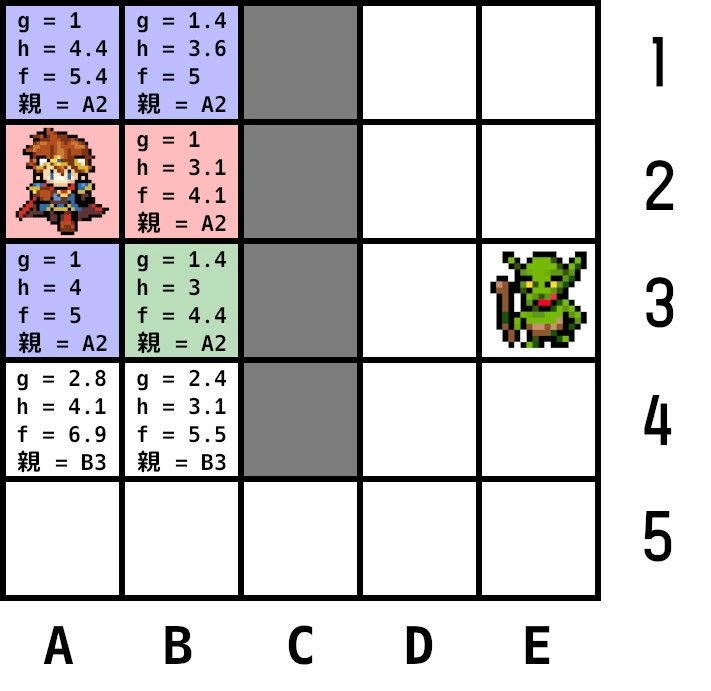
A3のgは再計算しても値が小さくならないため更新せず。A4、B4をオープンリストに追加し、それぞれに現在ノードを親として登録。
現在ノードをオープンリストから削除し、クローズドリストに追加。
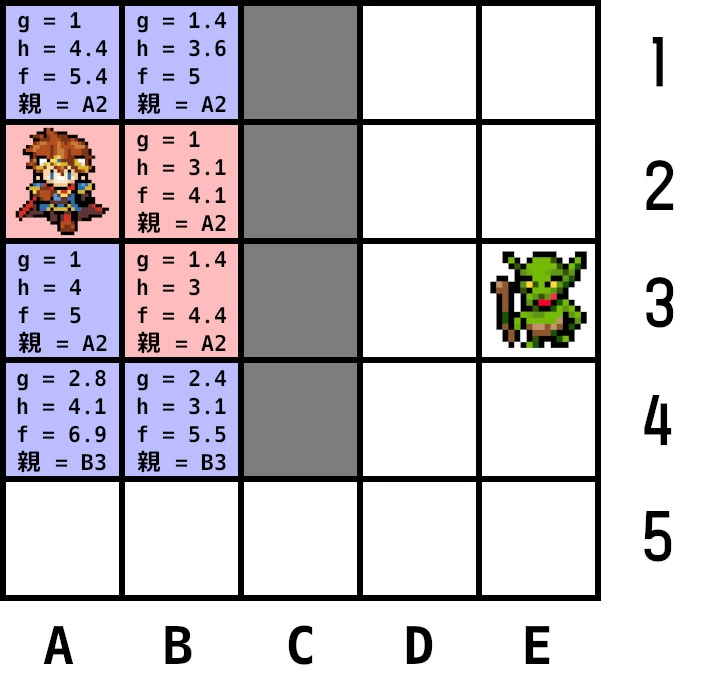
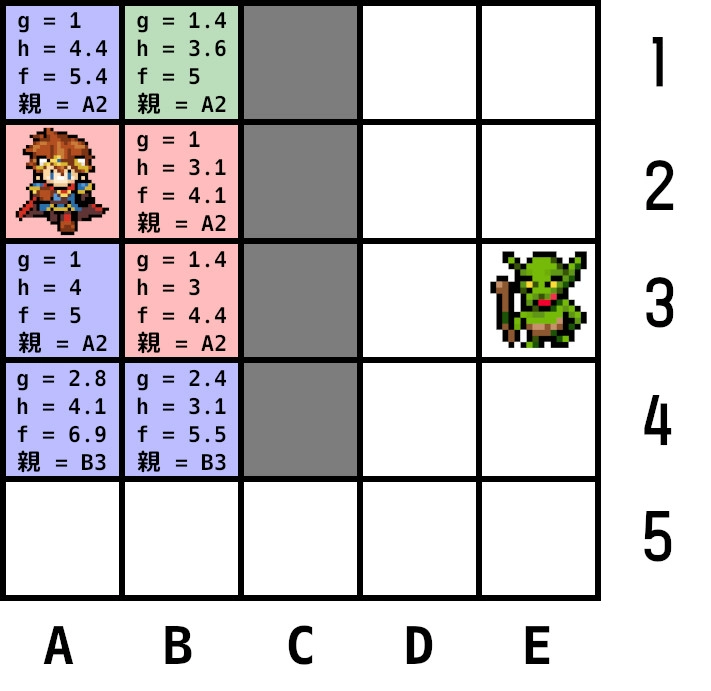
ここで手順2に戻りオープンリストから最小コストのノードを探すが、A3とB1が共にf=5で並んでいる。この場合、どのようなやり方でもよいのでどれかを選択する。
何かしらの方法によりB1が選ばれたとする。B1を現在ノードとし隣接ノードを計算する。左のA1のgを再計算してもgが元の値より大きいため更新しない。
現在ノードをオープンリストから削除し、クローズドリストに追加。手順2に戻る。
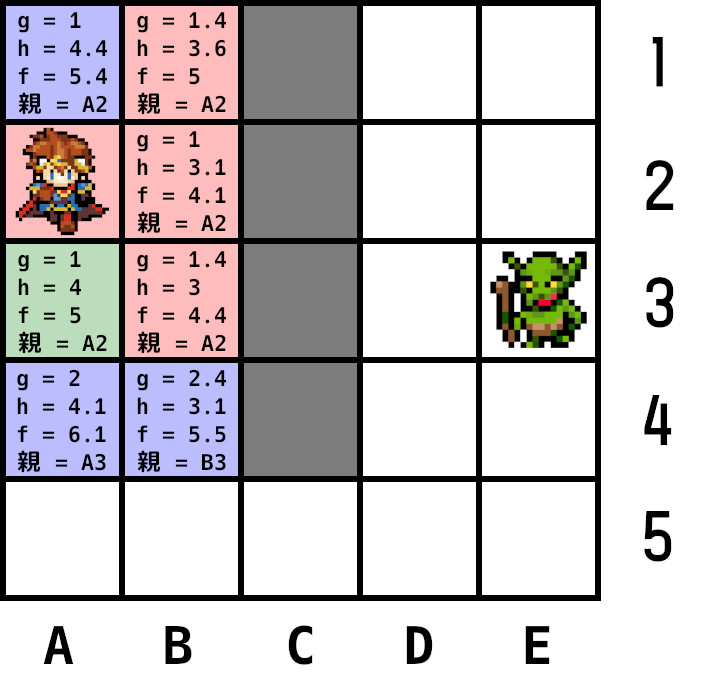
オープンリストから最小コストのノードを探すとA3。A4に対してgを再計算すると2、元の2.8より小さいため更新(fは6.1に)、さらに親ノードを現在ノード(A3)に再登録。
B4はgを再計算しても元のgより大きいため更新しない。
A3をオープンリストから削除し、クローズドリストに追加。手順2に戻る。
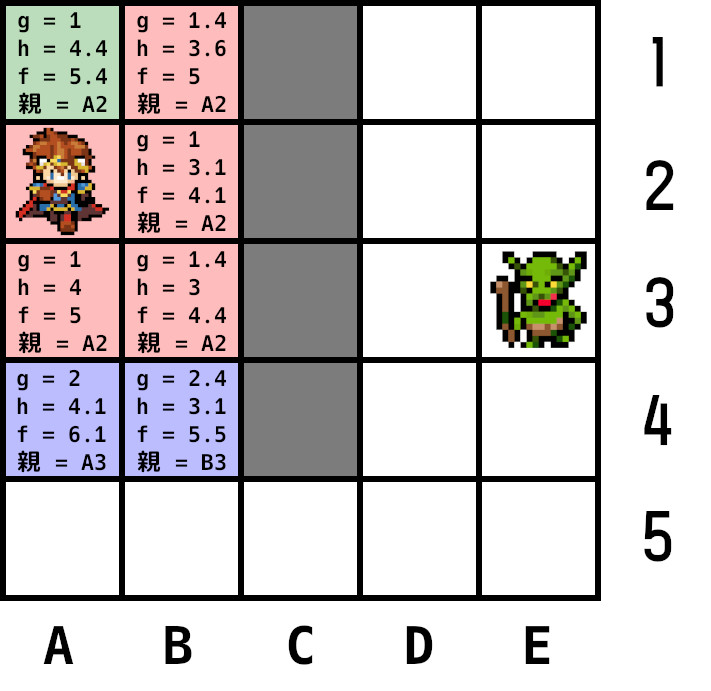
オープンリストから最小コストのA1を現在ノードに設定。隣接ノードは全てクローズドリスト追加済みのため何もしない。
A1をオープンリストから削除し、クローズドリストに追加。手順2に戻る。
次に選ばれたのがB4ノード。このノードを現在ノードにして、隣接ノードを計算する。
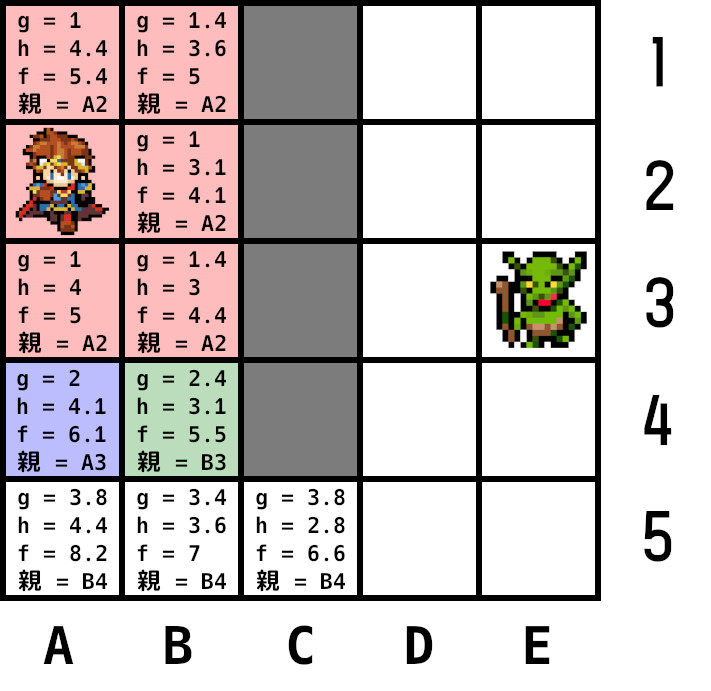
A4は再計算したgの値が元のgより大きいため更新しない。A5、B5、C5をオープンリストに追加し、現在ノードを親ノードとして登録。
現在ノードをオープンリストから削除し、クローズドリストに追加。
手順2に戻りオープンリストから最小コストのノードA4を選び、現在ノードにする。
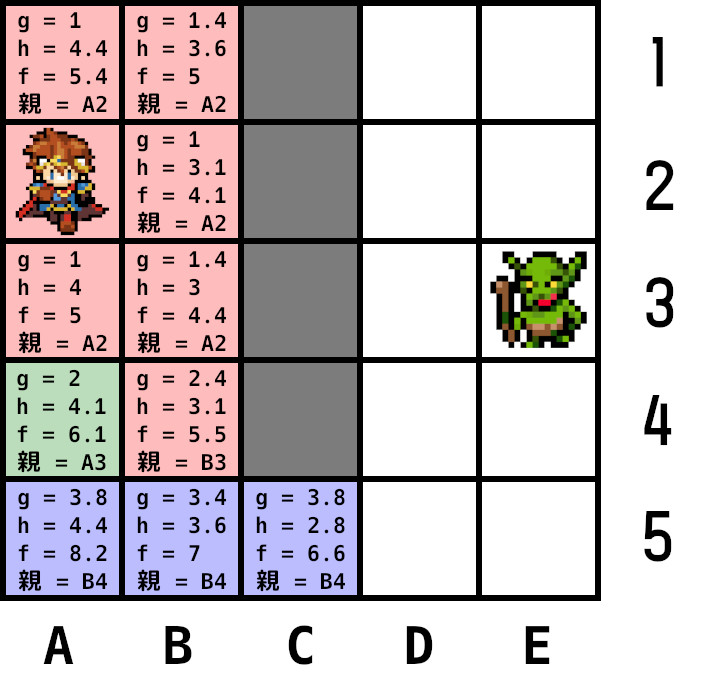
B4はクローズドリスト追加ずみのため無視。A5、B5は再計算したgが元のgより大きいため更新しない。
現在ノードをオープンリストから削除し、クローズドリストに追加。
手順2に戻り、オープンリストから最小コストのC5を現在ノードに設定。
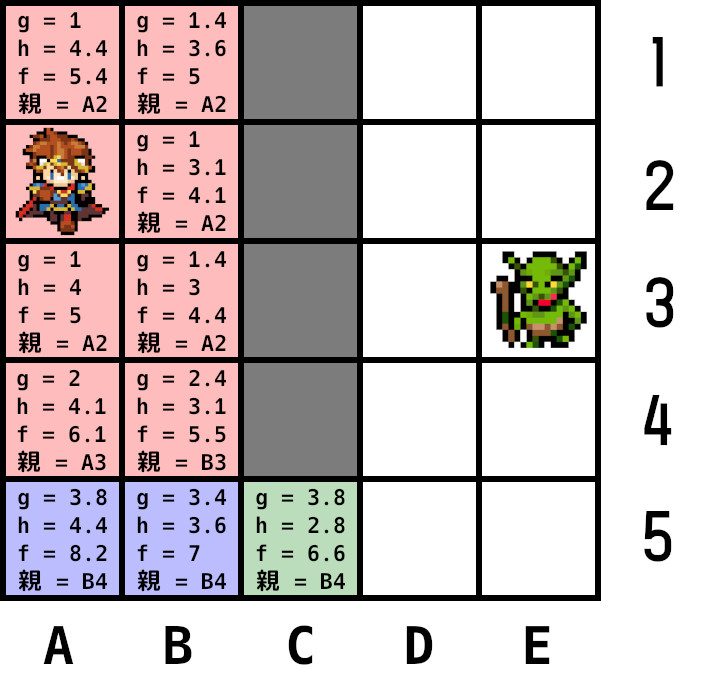
B4はクローズドリスト追加済みのため無視。B5は再計算したgが元のgより大きいため更新しない。残りのD4、D5を計算しオープンリストに追加し、現在ノードを親ノードとして登録。
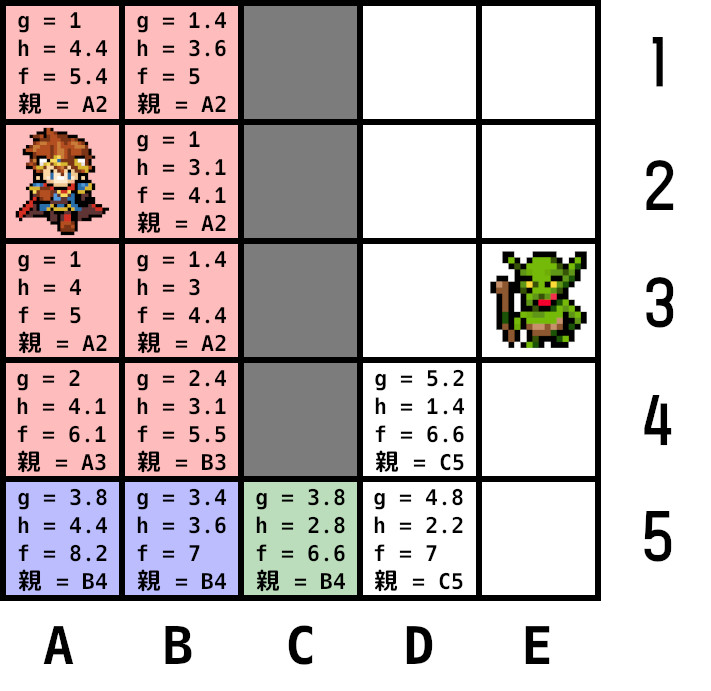
現在ノードをオープンリストから削除し、クローズドリストに追加。
手順2に戻り、オープンリストから最小コストのD4を現在ノードに設定。
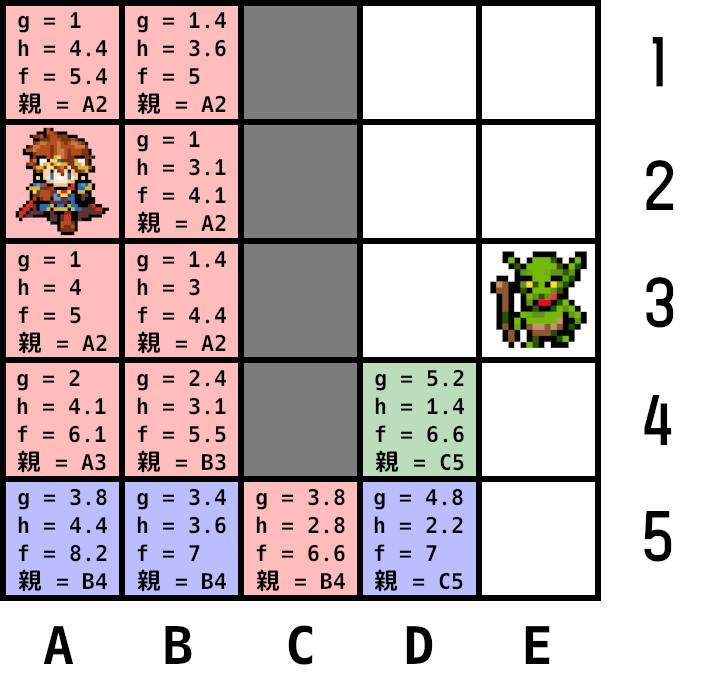
隣接ノードを調べる。D5は再計算したgが元のgより大きいため更新しない。D3、E3、E4、E5を計算しオープンリストに追加し、現在ノードを親ノードとして登録。
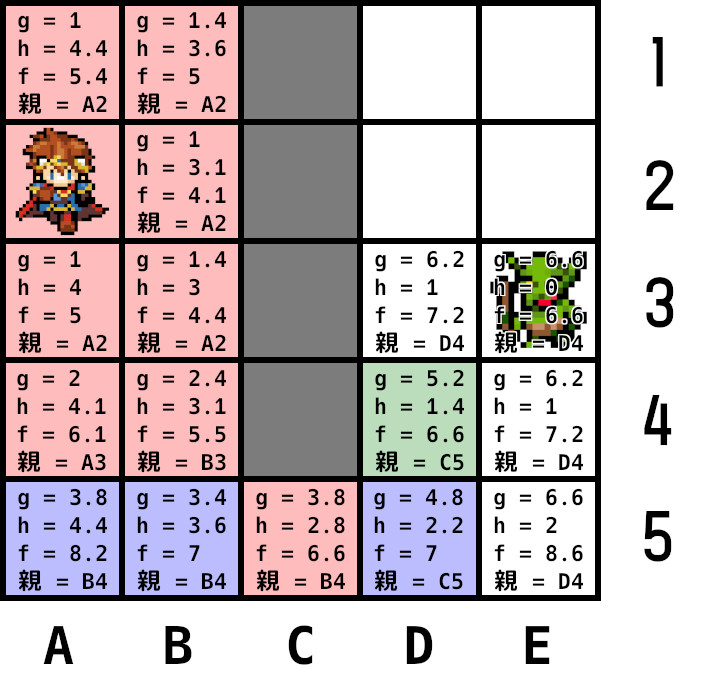
現在ノードをオープンリストから削除し、クローズドリストに追加。
手順2に戻り、オープンリストから最小コストのE3を現在ノードに設定。
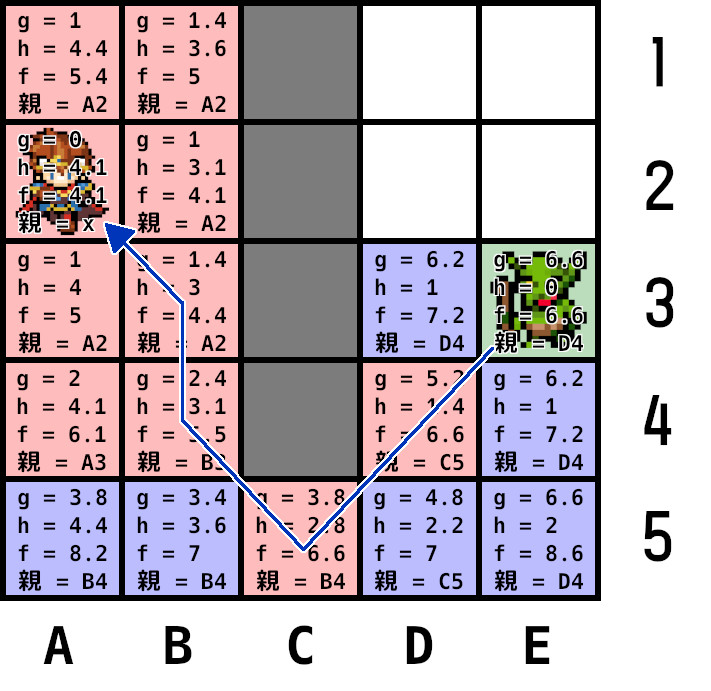
ここでE3がゴールであることが判明。ゴールノードに到着したら、ゴールノードの親ノードを調べ、さらにその親ノードの親ノードを調べを繰り返し最短経路を取得。
E3(ゴールノード)の親はD4、D4の親はC5、C5の親はB4、B4の親はB3、B3の親はB2、B2の親はA2(スタートノード)。経路は、
D4 → C5 → B4 → B3
となる。
極力、fコストの同値を防いで無駄な計算を省くには、小数第二位までを四捨五入して加えた方がいい。上サンプルも小数第二位まで含めると一度も同値にならない。
ゲームでA*アルゴリズムを利用する場合、ノードによって移動コストが異なる場合が考えられる。平地や川、沼や山などは同じ速度で移動できるとは思えない。この場合、平地は1、川や沼は2、山は3などと移動コストを変化させればよい。
参考図書

コメント